Nous allons prendre le problème à l’envers pour pouvoir réaliser ceci :

Le pivotement d’un objet par rapport à un point

- Oooohhh!!! - merci - Y’a pas de quoi. - Non, non vraiment… vous me génez

Dans le cas qui nous occupe maintenant, notre problème est inversé : nous connaissons les coordonnées de 2 points et nous devons calculer l’angle qu’ils forment. Pour ce faire nous allons voir une nouvelle fonction : la tangente.

---

Comprendre : la tangente d’un angle

Rappel : en trigonométrie, le rayon d’un cercle est toujours égal à 1.

Dessinons une première droite passant par le centre du cercle et faisant un angle alpha avec l’axe horizontal de ce cercle puis une seconde droite parallèle à l’axe vertical et passant par l’intersection de la circonférence et de l’axe horizontal du cercle.

La tangente de cet angle sera égale à la distance qui sépare l’intersection de ces deux droites de l’axe horizontal du cercle.

Si cette définition vous semble obscure, la figure ci-contre devrait vous éclairer. La tangente d’un angle est comprise entre 0 pour un angle de 0 degré et l’infini pour un angle de 90 degrés.

Calculer l’angle formé entre deux points

Nous n’allons pas utiliser la tangente directement (puisque nous ne connaissons pas l’angle entre nos deux points et que c’est ce dernier que nous voulons calculer) mais une fonction dérivée : l’arc-tangente.
L’arc-tangente permet de calculer un angle – compris entre 0 et 90 degrés – à partir des distances horizontales et verticales séparant deux points.

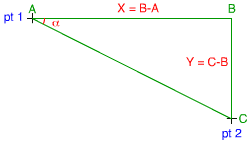
Reprenons le schéma représentant nos points 1 et 2. L’angle que nous recherchons sera égal à l’arc-tangente de Y/X.

Les valeurs X et Y sont faciles à obtenir dans Flash :

X = pt_2._x - pt_1._x;
Y = pt_2._y - pt_1._y;

L’arc-tangente est une méthode de l’objet Math. Par contre un arc-tangente ne se calcule qu’à partir de valeurs absolues (toujours positives). Nous allons d’abord calculer une valeur Z :

Z = abs(Y/X);

Puis calculer l’angle grâce à la fonction arc-tangente sans oublier de le convertir en degrés :

angle = Math.atan(Z) * 180 / Math.PI;

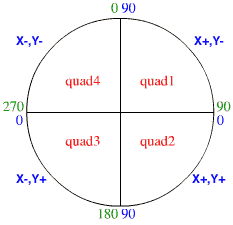Si nous reportons les arc-tangentes (en bleu) sur notre cercle, nous voyons que nous sommes confrontés à un triple problème :

- les arc-tangentes sont des nombres absolus.

- Les valeurs sont identiques dans chaque quart (quadrant) du cercle.

- L’origine d’une rotation dans Flash est située sur l’axe vertical et la rotation s’effectue dans le sens horaire (les valeurs de rotation sont indiquées en vert).

Nous allons donc déterminer dans quel quadrant du cercle se trouve notre angle. Pour cela nous allons utiliser les valeurs X et Y.
Ecrivons donc une petite conditionnelle :

if (X > 0 && Y < 0) {
quad = 1;
} else if (X > 0 && Y > 0) {
quad = 2;
} else if (X < 0 && Y > 0) {
quad = 3;
} else if (X < 0 && Y < 0) {
quad = 4;
}

Maintenant nous allons corriger l’angle selon le quadrant :

if (quad 1) {
angle = 90 - angle;
} else if (quad 2) {
angle = 90 + angle;
} else if (quad 3) {
angle = 270 - angle;
} else if (quad 4) {
angle = 270 + angle;
}

Il ne reste plus qu’à appliquer la transformation à notre objet

monObjet._rotation = angle;

---

Pour le plaisir, revoyons à nouveau le résultat. Vous remarquerez quelques erreurs dans l’affichage des résultats ; ils sont dus à l’arrondissement des nombres, mais n’altèrent en rien le comportement du clip.

Téléchargez le fla

Si vous souhaitez aller un peu plus loin

je vous propose deux exercices complémentaires à cet exposé :
- Mixez rotation et pivotement pour que l’objet tournant autour du cercle “regarde” toujours le centre
- Faites tourner l’objet sur une trajectoire ovoïde plutôt que circulaire