Une rubrique consacrée aux maths appliquées au multimédia.N’ayez pas peur, vous n’avez pas besoin de sortir de polytechnique…
Nous utiliserons des concepts mathématiques simples du niveau collège (mais comme c’est loin tout ça, un petit rappel ne fera pas de mal).
Un des principaux avantages de l’animation programmée comparée à l’animation image par image ou à l’animation interpolée est sa fluidité bien supérieure. L’autre gros atout, et non des moindres, est la simplicité avec laquelle on va modifier les paramètres de son animation. Grâce à la trigonométrie, nous allons déplacer des movie-clips sur des trajectoires circulaires et appliquer des rotations à des movie-clips.
Pour tous ceux qui ont préféré :
- lire Pif Gadget
- regarder les filles
- boire des bières en belgique
(rayez les mentions inutiles)
à la beauté obscure de la trigonométrie, voici quelques petits rappels indispensables.
(Pour les autres, il serait temps de – lire Pif Gadget – regarder les filles – boire des bières en belgique)
(rayez les mentions inutiles).
La beauté cachée
En mathématiques, les calculs sur les angles s’effectuent en radians et non pas en degrés. Pourtant lorsqu’on applique une rotation à une occurrence de movie-clip dans Flash avec la boîte de dialogue transformer on entre une valeur d’angle en degré. Et oui, notre Flash préféré converti gentiment pour nous les angles en degré. A contrario, si nous souhaitons effectuer une rotation calculée par le biais d’ActionScript nous devrons travailler en radians.Comprendre : la conversion des angles
Convertir des angles de degrés en radians est tout simple.
Voici les formules :
angleEnRadians = angleEnDegrés*PI/180 angleEnDegrés = angleEnRadians/PI*180
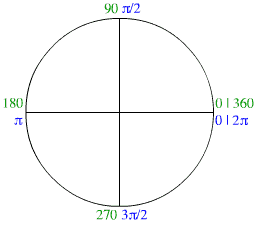
Facile !! Ce qui nous donne le petit schéma ci-contre
Attention : en trigonométrie, la rotation a lieu dans le sens contraire des aiguilles d’une montre et l’origine est sur l’axe horizontal. les angles exprimés degrés sont en vert et les angles exprimés en radians en bleu.
Rotation d’un point sur la circonférence d’un cercle
Dans cet exemple, nous allons déplacer un movie-clip sur une trajectoire circulaire.
Pour réaliser cette animation, nous allons calculer à chaque image la position de notre balle selon un angle avec l’axe horizontal que nous augmenterons de 1 degré jusqu’à ce qu’elle ait fait un tour complet.
Les plus observateurs me feront remarquer que la balle ne tourne pas selon le sens du schéma ci-dessus.
La cause de ce retournement vient de Flash. En effet, l’axe vertical est inversé : l’origine de l’axe vertical est sur le bord supérieur de la scène et les valeurs verticales augmentent en allant vers le bas.
mais commençons par écrire le script du bouton :
on(release){
// initialise l'angle
_root.monAngle = 0;
}
puis le script du clip balle
onClipEvent(load){// bloque l’animation jusqu’au clic bouton
_root.monAngle = 360;
}onClipEvent(enterFrame){
// stoppe l’animation à la fin d’un tour complet
if(_root.monAngle < 360){// augmente l’angle de 1 degré
_root.monAngle += 1;// converti l’angle en degré
monAngleConverti = _root.monAngle * Math.PI / 180;
}
}
Reste à déplacer la balle.
Pour cela nous aurons besoin de deux fonctions trigonométriques : sinus et cosinus.
Comprendre : sinus et cosinus d’un angle
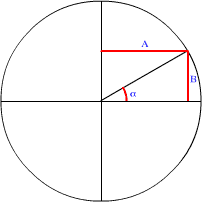
Dessinons une droite passant par le centre du cercle et faisant un angle alpha avec l’axe horizontal de ce cercle. Le sinus de cet angle sera égal à la distance qui sépare l’intersection de cette droite avec la circonférence du cercle et l’axe vertical ; le cosinus de cet angle sera égal à la distance qui sépare l’intersection de cette droite avec la circonférence du cercle et l’axe horizontal.
Dans la figure ci-contre, le sinus de alpha est égal à la distance A et son cosinus à la distance B.
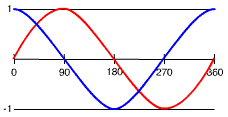
Comme le rayon du cercle est égal à 1, le sinus d’un angle varie de -1(270 degrés) à +1(90 degrés) avec une valeur de 0 pour les angles de 0 degré et de 180 degré.
Le cosinus d’un angle varie lui aussi entre -1 et +1 : cos(0)=1, cos(90)=0, cos(180)=0, cos(270)=-1
on retrouve donc la courbe des sinus en rouge et celle des cosinus en bleu.
Utiliser les fonctions sinus et cosinus de Flash.
Reprenons le script du clip balle. Nous allons rajouter deux nouvelles lignesthis._x = Math.sin(monAngleConverti); this._y = Math.cos(monAngleConverti);
Comme les valeurs que nous venons de calculer varient entre -1 et +1, nous devons les multiplier par le rayon de notre cercle (puisque notre cercle n’a pas un rayon de 1 mais de n pixels). Le centre de notre cercle possède également une position horizontale et verticale sur la scène. Pour faciliter les modifications de cette animation, nous allons transformer notre cercle en symbole de clip. Nos deux lignes deviendront :
this._x = Math.sin(monAngleConverti) * (cercle._width/2) + cercle._x; this._y = Math.cos(monAngleConverti) * (cercle._width/2) + cercle._y;
Voici une variante. Au lieu d’effectuer un tour complet, nous allons positionner le clip sur le cercle selon un angle choisi par l’utilisateur.
Maintenant que vous êtes accro, allez vite découvrir la suite. Nous allons inverser le problème. Au lieu de faire tourner un clip autour d’un point, nous allons faire tourner ce clip sur lui même pour qu’il “regarde” toujours la souris.
